W paragrafie 2.1 ustaliliśmy, że prędkość światła jest
jednakowa we wszystkich układach odniesienia. Pociąga to za sobą pewne
konsekwencje. Np. światło we wszystkich układach odniesienia jest falą
kulistą (czoło znajduje się zawsze o ![]() od punktu centralnego). Piszemy
więc równanie kuli:
od punktu centralnego). Piszemy
więc równanie kuli:
| (2.1) |
Zapiszemy to teraz dla innego układu współrzędnych, przemieszczającego się
względem oryginalnej osi ![]() z prędkością
z prędkością ![]() . Zrobimy jeszcze uogólnienie,
że czas w ruchomym układzie zależy od położenia tego układu względem
obserwatora (
. Zrobimy jeszcze uogólnienie,
że czas w ruchomym układzie zależy od położenia tego układu względem
obserwatora (![]() ) i obliczymy niewiadomą l.
) i obliczymy niewiadomą l.
Niewiadoma ta byłaby dla transformacji galileuszowskich jest równa zero, ale tutaj zerowa być nie może. Spójrzmy na równanie:
To równanie nie może być spełnione dla dowolnego ![]() przy niezmodyfikowanym
czasie! Wnioskujemy więc, że musi zależeć jeszcze od położenia.
Lecimy więc dalej:
przy niezmodyfikowanym
czasie! Wnioskujemy więc, że musi zależeć jeszcze od położenia.
Lecimy więc dalej:
| (2.3) | |||
| (2.4) | |||
![$\displaystyle c^2t^2(1-\frac{v^2}{c^2})=x^2[1-(lc)^2]-\underbrace{2tx(v+c^2l)}_{fe}+y^2+z^2$](img43.gif) |
(2.5) |
W ostatnim równaniu obraz równania kuli zaburza podkreślony czynnik. Jednak wiemy, że światło ma prędkość stałą we wszystkich układach, więc czynnik ten musi być równy zero. Z tego wynika nam
| (2.6) |
Podstawiając do wzoru na falę kulistą, otrzymujemy:
| (2.7) |
Co określa z punktu widzenia układu obserwatora rozchodzenie się fali kulistej w układzie ruchomym. Obserwator w układzie ruchomym oczywiście widzi upływ czasu i rozchodzenie fali bez tego śmiesznego współczynnika, czyli
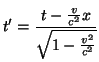 |
(2.8) | ||
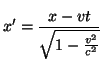 |
(2.9) |
W powyższym wzorze od razu podany został też wzór na ![]() . W miejscu
. W miejscu ![]() oraz
oraz
![]() po prawej stronie, podstawione zostały już ostatecznie funkcje
po prawej stronie, podstawione zostały już ostatecznie funkcje
![]() oraz
oraz ![]()
Powtarzając całe rozumowanie, zamieniając we wzorach prędkość ![]() na
na ![]() ,
dostaniemy przekształcenia odwrotne; z układu poruszającego się do
spoczywającego:
,
dostaniemy przekształcenia odwrotne; z układu poruszającego się do
spoczywającego:
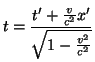 |
(2.10) | ||
 |
(2.11) |
Są to transformacje Lorentza.
Można się teraz pokusić o obliczenie prędkości mierzonej w układzie
spoczywającym (
![]() ), znając prędkość w układzie
ruchomym (
), znając prędkość w układzie
ruchomym (
![]() ), poruszającym się z prędkością
), poruszającym się z prędkością
![]() względem obserwatora nieruchomego:
względem obserwatora nieruchomego:
| (2.12) |
(mianowniki nam się w liczniku i mianowniku uprościły) Wyciągamy teraz
![]() przed nawias mianownika
przed nawias mianownika
| (2.13) |
Jest to wzór na relatywistyczne składanie prędkości. Jak widać, nie ma możliwości przekroczenia prędkości światła.
Powyższe wyprowadzenia są bardzo proste, ale bardziej trafiające do wyobraźni jest przypuszczalnie podejście geometryczne, z diagramami czasoprzestrzennymi. Może kiedyś pojawi się rozdział i o tym.