![\includegraphics[height=4cm,width=6cm]{przyspieszenia.eps}](img228.gif)
|
Spójrzmy na rysunek 3.1. Mamy tam dwa układy: inercjalny oraz nieinercjalny, który porusza się względem inercjalnego z pewnym przyspieszeniem. Przeprowadźmy pewne różniczkowanka.
| (3.1) | |||
 |
(3.2) |
Mamy tu na początku zapisany wektor położenia punktu P z pomocą wektorów
jednostkowych ![]() układu inercjalnego i
układu inercjalnego i ![]() układu nieinercjalnego.
Wykonując różniczkowanie, pamiętamy że orientacja wektorów jednostkowych
układu nieinercjalnego może ulegać zmianie, a więc zależy od czasu.
Różniczkowaniu podlega więc funkcja
układu nieinercjalnego.
Wykonując różniczkowanie, pamiętamy że orientacja wektorów jednostkowych
układu nieinercjalnego może ulegać zmianie, a więc zależy od czasu.
Różniczkowaniu podlega więc funkcja
Otrzymaną pochodną możemy zapisać jako:
| (3.3) |
Tzn. mamy pochodną iloczynu. Różniczkując to wyrażenie dalej, dochodzimy do:
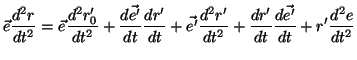 |
(3.4) | ||
| (3.5) |
W ostatnim równaniu poszczególne człony mają następujące znaczenie:
 |
(3.6) | ||
 |
(3.7) | ||
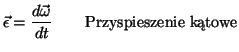 |
(3.8) | ||
| (3.9) | |||
| (3.10) | |||
| (3.11) | |||
| (3.12) | |||
| (3.13) |
Widać stąd m.in, że siła Coriolisa nie jest niczym magicznym i wynika wprost z rozważań nad układem nieinercjalnym i jego zachowaniem względem układu inercjalnego.