W mechanice kwantowej wielkości mierzalne oblicza się w sposób specyficzny.
Należy tu w jakiś sposób zadziałać na wektor stanu (który spełnia równanie
fali), aby uzyskać interesującą wartość. Jest tak, bowiem wszystkie
informacje trzeba właściwie wyciągać z funkcji falowej. W tym celu przypisuje
się wielkościom mierzalnym operatory.
Wielkości mierzalnej ![]() odpowiada operator
odpowiada operator
| (6.4) |
gdzie ![]() to możliwe wektory stanu w całej przestrzeni. Operator
działając na wektor zwykły daje w wyniku wektor zwykły, działając na wektor
dualny, daje wektor dualny:
to możliwe wektory stanu w całej przestrzeni. Operator
działając na wektor zwykły daje w wyniku wektor zwykły, działając na wektor
dualny, daje wektor dualny:
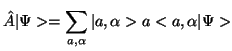 |
(6.5) | ||
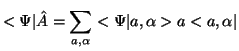 |
(6.6) |
Działając obecnie operatorem ![]() na wektor stanu
na wektor stanu ![]() ,
korzystając z ortonormalności bazy
,
korzystając z ortonormalności bazy ![]() (tj.
(tj.
![]() ), uzyskamy
), uzyskamy
| (6.7) |
Co oznacza, że aby obliczyć wielkość mierzalną ![]() , należy obliczyć
wartość własną powyższego równania dla wektora własnego
, należy obliczyć
wartość własną powyższego równania dla wektora własnego ![]() .
Pamietamy bowiem z matematyki, że równanie własne oznaczało się tam jako
.
Pamietamy bowiem z matematyki, że równanie własne oznaczało się tam jako
| (6.8) |
gdzie ![]() było macierzą, a
było macierzą, a ![]() wektorem własnym, natomiast
wektorem własnym, natomiast
![]() było skalarną wartością własną. Powyższe równanie operatorowe ma
identyczną strukturę, jedynie operator nie jest jako taki macierzą. Jednak
można operator przedstawić również w postaci macierzy, działając nim na
wektory bazowe wektora stanu,
było skalarną wartością własną. Powyższe równanie operatorowe ma
identyczną strukturę, jedynie operator nie jest jako taki macierzą. Jednak
można operator przedstawić również w postaci macierzy, działając nim na
wektory bazowe wektora stanu,
| (6.9) |
(działamy tu operatorem na kolejne wektory bazowe ![]() , a następnie
rzutujemy całość na dualne wektory bazowe
, a następnie
rzutujemy całość na dualne wektory bazowe ![]() ). W efekcie uzyskujemy
klasyczne równanie własne.
). W efekcie uzyskujemy
klasyczne równanie własne.